新里曼理论➊:PLR操作和音网图
分享
上一节功能和声的变迁➋中提到了受里曼启发的理论家们(主要是美国的)发展了在一定程度上继承了里曼想法的理论。这些理论被统称为新里曼理论(英 Neo-Riemannian Theory)。这一领域在21世纪仍有激烈的争论,是一个还在不断发展的理论。
本节将介绍新里曼理论的主要研究。
1
变形的理论
首先,正如功能和声的变迁❶中说明的那样,里曼对许多和弦给予了以TDS和弦为基础的关联性的符号。
其特征如图所示,Cm、Am和Em都是与C之差一个音的和弦,这意味着和弦是通过“移动”来构建的。里曼的理论是为这种变形操作在原有和弦符号基础上增加标记,他试图做的是创建一个和弦符号系统来取代罗马数字符号。
然而,新里曼理论对此有异议。既然移动的概念很有趣,那么最好使用Relative和Leadingtone-change等词作为移动操作(operation)的名称,而不是和弦的名称。新里曼理论的先驱戴维·勒温(David Lewin)对里曼的批评相当尖刻,他批评里曼提出了和弦变形的思想,却没有将其作为“变形的理论”提出来。
An even more basic problem for Riemann was that he never quite worked through in his own mind the transformational character of his theories. He did not quite ever realize that he was conceiving “dominant” (whether DOM or DOM′) as something one does to a Klang, to obtain another Klang. Here, I conjecture, he was unduly influenced by a desire to promote his notation as a substitute for Roman-Numeral notation;
里曼的另一个更基本的问题是,他从来没有完全在自己的脑海中思考过他的理论的变形性质。他从来没有意识到,他在构想的“属和弦”(无论是DOM还是DOM′)是一种对一个和弦操作,以获得另一个和弦。在这里,我推测,他受到了一种促使他的记号取代罗马数字记号的欲望的不当影响;
Lewin, David. Generalized Musical Intervals and Transformations (p.177).
连他的雄心壮志都被贬低了,听起来十分尖锐。但其他评论家也有类似的指摘1
例图
这真是一条出于爱的diss,“这么有趣的话题不深入研究真是浪费!”新里曼理论试图基于里曼的思想将和弦变换系统化。
这种“从和弦本身的符号化到和音变形操作的符号化”的范式转换是新里曼理论思想的核心,恐怕这也是冠以“新”之名的原因。
这与“连接系统理论”中观察和弦之间的变化而非排列和弦本身相似。通过改变分析方法,我们可以发现与以往不同的东西。新里曼理论也会给我们带来新的启示。
3种基本的变形操作
新里曼理论中的典型变形操作是上图中与C⇄Cm、C⇄Em和C⇄Am相对应的。
同主调关系的和声之间替换的Parallel、大三度关系和声之间替换的Leadingtone-exchange、还有平行关系调和声之间替换的Relative,是直接从里曼的功能名拿了过来的。它们有时被缩写为 PAR、LT和REL,但更常见的写法是用单个首字母P、L和R。在新里曼理论体系的许多研究中,这三种操作被定义为基本操作。
声部连接的简约
如你所见,P和L只移动半音,R也只移动一个全音,声部的移动相当顺畅。例如用五度圈的理论来说,C和Em是通过E→A→D→G→C这四次五度链连接起来的遥远的存在,然而,通过重新思考,将它们视为只差一个半音就能到达的熟悉的实体,并引入不同的和弦进行的价值体系,新里曼理论具有一定的意义。
这种方法强调以声部的运动量而不是以根音的运动量来衡量和弦之间的联系,被称为声部连接的简约(英 Voice-Leading Parsimony)2
里曼描绘的镜像世界
关于 PLR 的操作,根据大小和弦的不同操作内容是相反的。对于大和弦,R的操作是将5th升高一个全音,而对于小和弦是完全相反的,R的操作是将Rt降低一个全音。因此,虽然我们说的是“三种基本操作”,但实际上有六种变形模式。
首先,为什么要创建如此复杂的方法论,以至于大小和弦的处理方式不同?这和上次谈到的“和声二元论”的想法有关。里曼认为小和弦是大和弦的完全上下反转,甚至说小和弦的根音是5th。由于所有定律都是相反的,里曼将P、L和R的大小完全颠倒过来是合情合理的。
和声的操作是美丽的镜像
当然,新里曼理论的论者基本上废除了“5th根音说”,但由于这种和声二元论的起源,所以它成为了一个大小和弦颠倒转换的独特体系。结果,PLR操作都伴随着和弦的大小转换,而且重复2次就会恢复原来的和弦。这里也能感受到“乘以负数两次就会回到正数”的即视感。
PLR操作和根音变化
现在,尽管我们说我们将C-Em视为半音阶移动而不是3度上行,我们仍然好奇这些操作实际上会移动根位置多少。再一次,如果我们将转位重新排列为基本形,并检查根音在每转换中的变化情况,我们可以看到如下结果。
这样看,我们可以看到,基本操作中只使用了大、小三度连接,上下行中也缺少一向(例如,大和弦的小三度上行不包含在基本操作)。显然,这是一个世界观非常奇怪的理论。
这也难怪,里曼首先将T和弦上下的五度和弦确定为D和S,当他思考如何处理其他和弦时,他想出了平行和弦和导音转换。因此,这里没有五度变换是必然的结果。
此外,由于里曼一开始是用符号表示调内的和弦,所以没有自然音阶中的“大和弦小三度上行”的符号。当然,也有新里曼主义者反对这个系统的扭曲,但我稍后会讨论这一点。
5度和2度呢?
如果我们仅将此PLR操作视为和弦进行的“元素”,则5度或2度的进行将被标记为多个操作的组合。
这样,以L·R的顺序对C进行变形则为G,反之以R·L的顺序进行变形则为F。因此,在新里曼理论中,从Maj到Maj的完全5度上行表示为LR,完全5度下行表示为RL。如果min→min或min→Maj的话,顺序又会改变,所以这方面相当繁琐。
而2度上行时,因为没有共同音符,所以至少需要三步才能到达。
在上面的C-Dm和F-Em的例子中,都是3个动作,但根据和弦性质等情况,可能需要额外添加一个P操作。
D操作
果然只有3度的连接作为“元素”太弱了吧?因此,有些人把5度下行作为DOM,或者记作D,作为基本的变形3
因为2度下行D了2次,所以标记为D²,又或者5度“上行”的话,因为与D操作相反,所以标记为D⁻¹等,就像在模仿数学的标记。
关于D操作的风格并不统一,有些人认为不使用D是因为PLR已经足够,而另一些人则认为使用D操作会更方便。
S操作、N操作
有共同音的和声的连接还有很多组合,如果想起名字的话,可能数不胜数。其中获得一定地位的是SLIDE(S)4
“Nebenverwandt”在英语中时“Next-related”的意思。确实,如果用半音数来考虑声音的移动量的话,两个半音的移动就等价于R操作的一个全音移动,所以给它起个名字也不错吧。关于N操作,不仅是I-iv的进行,古典小调的cadence III-vi也可以用一个字来记述,这一点采用的话好像很方便。
总而言之,新里曼理论将三度连接特权化,而其他连接则是次要的。但是,3度连接与I-IV-V-I和vi-ii-III-vi等基本cadence毫无关系,在传统的和声理论中,3度连接显得有些单薄,这样优先连接有意义吗?
2
分析对象
新里曼理论的主要目标音乐流派是19世纪浪漫主义古典音乐6
这是1887年创作的勃拉姆斯的《小提琴和大提琴双重协奏曲》。从270小节安静的部分,可以看到包含多次同主调的转换的不可思议的进行。分析和声的话,如下所示。
这绝不是传统的进行,但却有其规律和美感。三度连接……。这就是新里曼理论的用武之地:如果用PLR的转换操作理论来分析,你会发现……
竟然出现了PLPLPLP这一有规律的字符串!这是新里曼理论的分析非常奏效的典型例子。按照以往的理论G♯m-E, Em-C看作一套,是一边大3度转调一边重复,不过,从TDS的功能感和度数的角度来讨论的话,就有点微妙了,在由于没有五度进行而调性尚未明确确立的情况下,不断地转调,在某种程度上感觉像是脱离了歌曲的本质。 而解释称“PLPLPLP”的话,因为音阶变化连接是通过平行过渡连接的,无需根音移动,这是一个非常“节俭”的进行,在整个进行过程中仅移动半音差异,都能清晰地传达出来。
这是贝多芬的“第九”或《第九交响曲》的第二乐章,创作于1824年,因其第四乐章而著名。在典型的V-I cadence之后,是连续的三度下行,C-Am-F-Dm(I-vi-IV-ii),然后是三个小节的完全休止。ii之后接下来进入V是古典派的“约束”,但令人大吃一惊的是Dm-B♭-Gm-E♭,接着三度的下降!然后,在又一个三小节的休止符后,从E♭开始又是一个急促的三度下降。可以用新里曼理论来分析和弦A之前的一连串进行……
居然是,RLRLRL RLRL RLRL RLRL。可以看到,这只是一系列的RL而已!
按照传统理论,这也可以看作是I-vi-IV-ii的连续,但是对于有规律的大和弦和小和弦的重复,一个是I-vi,另一个是IV-ii,这样的划分有点不合理。总有一种故意的感觉,感觉是想把作品嵌进调性音乐的模子里去解释。如果说哪一种能更明快地凸显贝多芬在此所构筑的有规律的进行之美,那么新里曼理论应该更胜一筹吧。
第三章的最后我们谈到了被称为“Chromatic Midiant”的非调性3度进行在电影音乐中被活用。这样的音乐也是新里曼理论擅长的范畴。
此外,在摇滚音乐中,C-E♭和C-A♭等不符合传统调性的三度进行也有存在,因此有论文用新里曼理论分析Radiohead和Ozzy Osbourne的摇滚歌曲。
因此,专门针对三度进行的理论可能确实过于局限,无法成为主要武器,但它却是某些音乐,尤其是某些情况下的最佳分析工具。这与埃内·伦德瓦伊(Erne Lendvai)的轴心体系如何补充三度音程关系的理念相似。
PLR变形操作是新里曼理论最具代表性的内容,另外还包括一些有趣的研究,在此也进行介绍。
3
音网图(Tonnetz)
里曼在之前提到的《Harmony, Simplified》出版后继续更新他的理论,并于 1916 年出版了《Ideen zu einer 'Lehre von den Tonvorstellungen'》一书,日文译名为《音想像論》。
在对音乐接收者心理进行考察的同时,将声音关系图形化和数字化。其中之一就是音音网图(英 Tonnetz),它把音阶像网一样连接在一起7
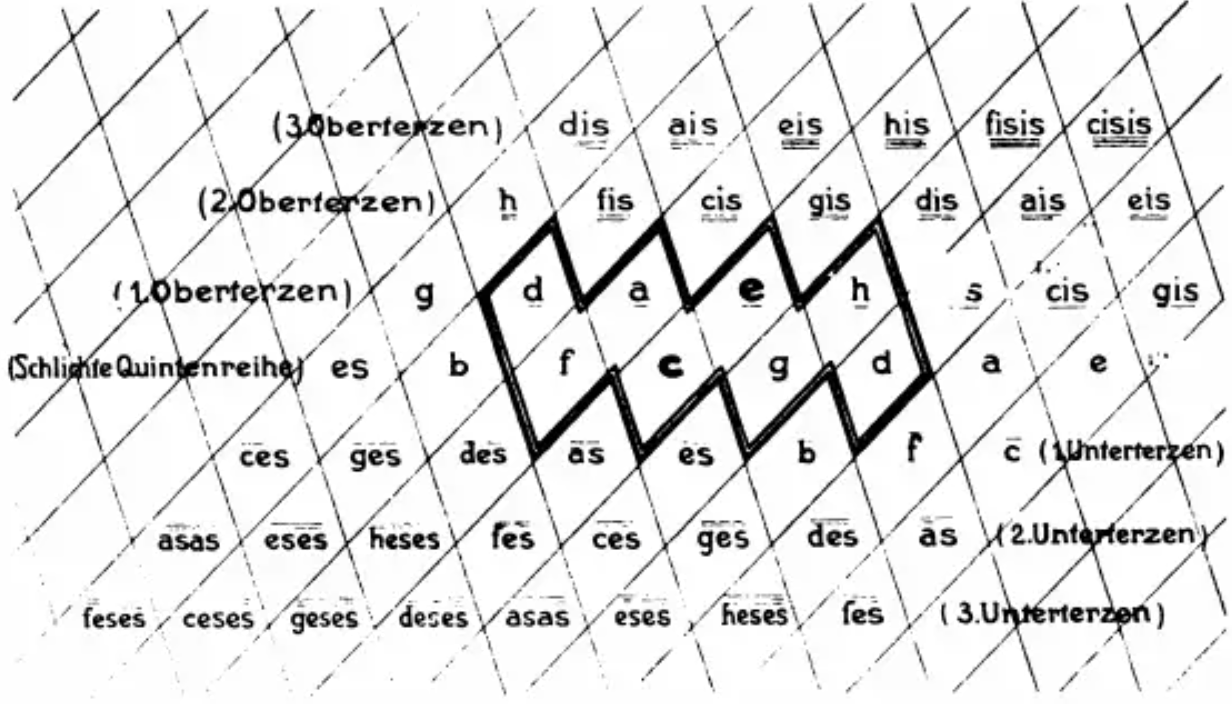
Riemann, Hugo. Ideen zu einer ‘Lehre von den Tonvorstellungen’.
Tonnetz在英语中的意思是Tone的Net,也就是“音的网”。首先以c为中心看的话,左右有f和g,这是和五度圈一样的完全5度的排列。看上面一层,声音和g-d-a-e有5度关系。再从c看右上和左下的斜线,e-c-a♭和这个是大3度关系。反之,左上和右下角的斜线是a-c-e♭,这个是小3度关系。像这样,根据5度和3度的关系,以二维的方式图示了声音的网络就是音网图。
到目前为止,说到声音关系的图示,都是“五度圈”,但五度圈只是用一条线将声音连接成圆形,所以当然只明确了五度关系。与此相对,音网图将声音用纵横2轴进行二维排列,不仅是5度关系,连大3度、小3度的关系也可视化了。因此,不难想象它的用途会更加广泛。
现在常见的音网图
音网图的本质是“横轴以5度为间隔,纵轴以3度为间隔”,具体的可视化方法有很多变化。有的不是斜的,而是尖锐的长方形格子状,也有的上下方向相反。另外,异名同音的区别也因人而异。
无论如何,后来的理论家们在新里曼理论中普遍推广的一种改进是,不再将声音写在网格中,而是将其放在网格的交叉点上,从而形成了一种声音通过线条相互连接的构图。
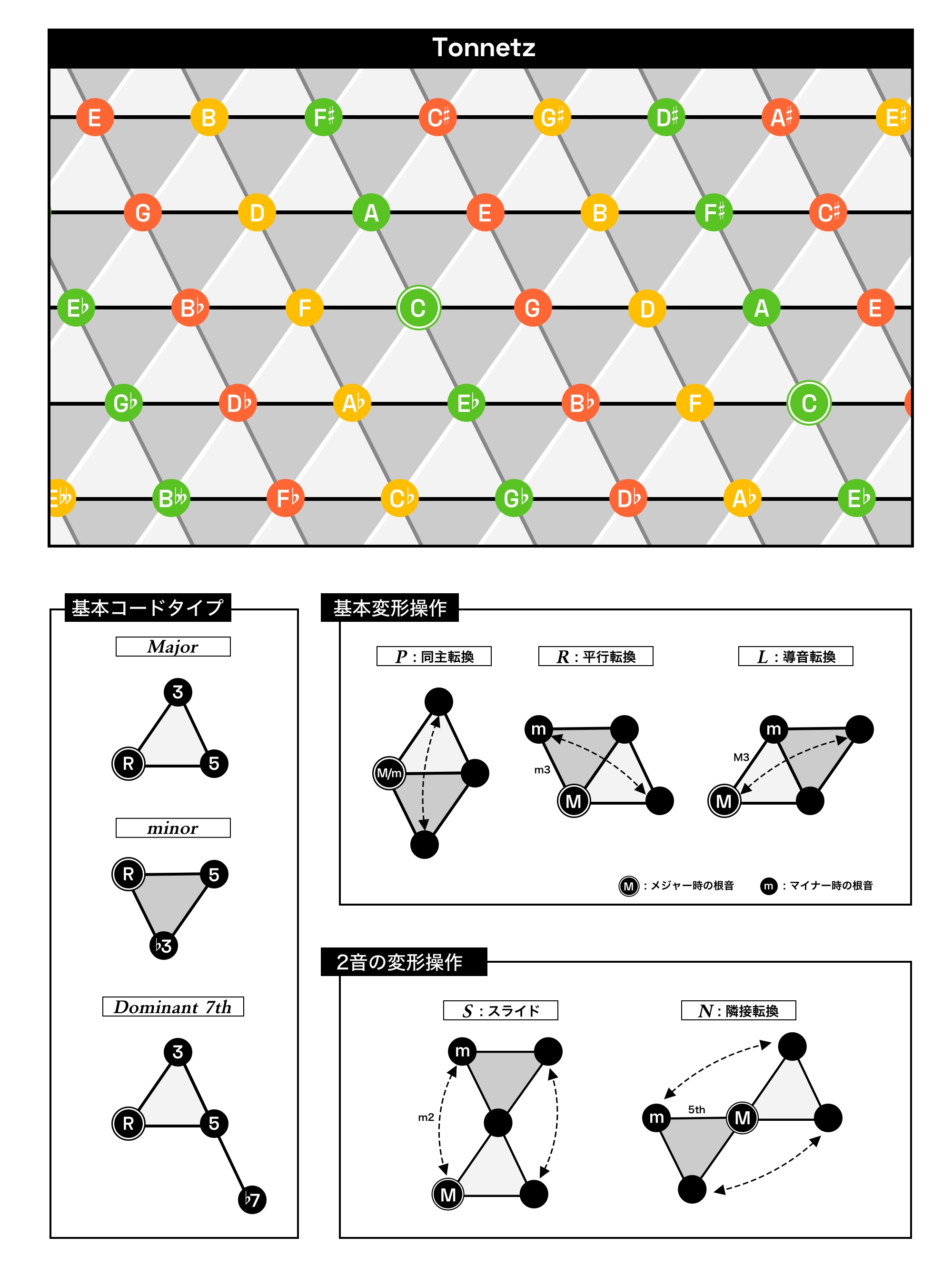
现代常见的音网图的形状(配色根据本网站)
因为信息量有点大,所以按顺序说明一下,首先用线连接音,然后连接大和弦和小和弦的音,就会画出三角形。因此,图中的三角形方格本身就是和弦的象征。例如连接C、E、G三点的直线所描绘的三角形格就是C大和弦的格。并且PLR的操作对其他代和弦的变形都表现为将这个格移动1格的行为。附带的S·N操作,也像翻转沙漏一样,以漂亮的对称运动来表示。
音网图绝非只能在新里曼理论中使用,但由于它的结构,所有PLR操作都会转移到相邻的音块上,因此该图非常适合新里曼理论,因为新里曼理论非常重视这些操作。例如,前面提到的贝多芬C-Am-F-Dm的和弦进行可以在音网图上表示如下。
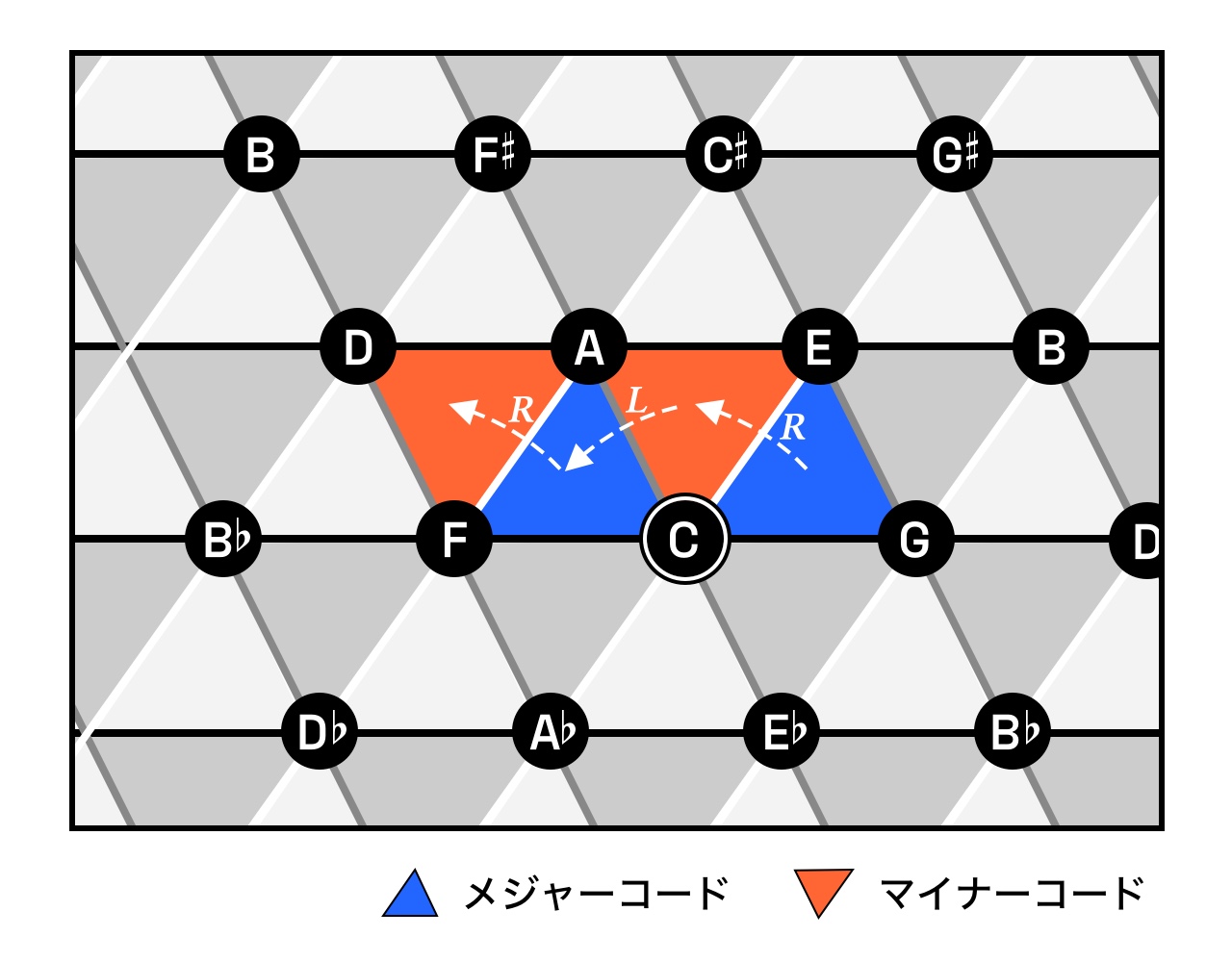
这样,和弦进行就可以用空间和图形来表达,就好像双陆棋的方格进行一样。声部连接越“节俭”,路径的三角关系就越紧密、越优美。显然,这意味着我们可以做各种有趣的事情!就像五度圈可以用来表示调性的增减或寻找基本和弦一样,像这样的多功能图画在练习和分析中都是非常有用的。
和弦版音网图
音网图是一幅以单音为点,以面和线来表示和音的图画,这样一来,人们就会产生这样的想法:如果每个点都以和弦的形式来表示,那么在讨论和弦的时候,是不是就能更紧凑地总结了呢?当然这也被具体化了,如下图。
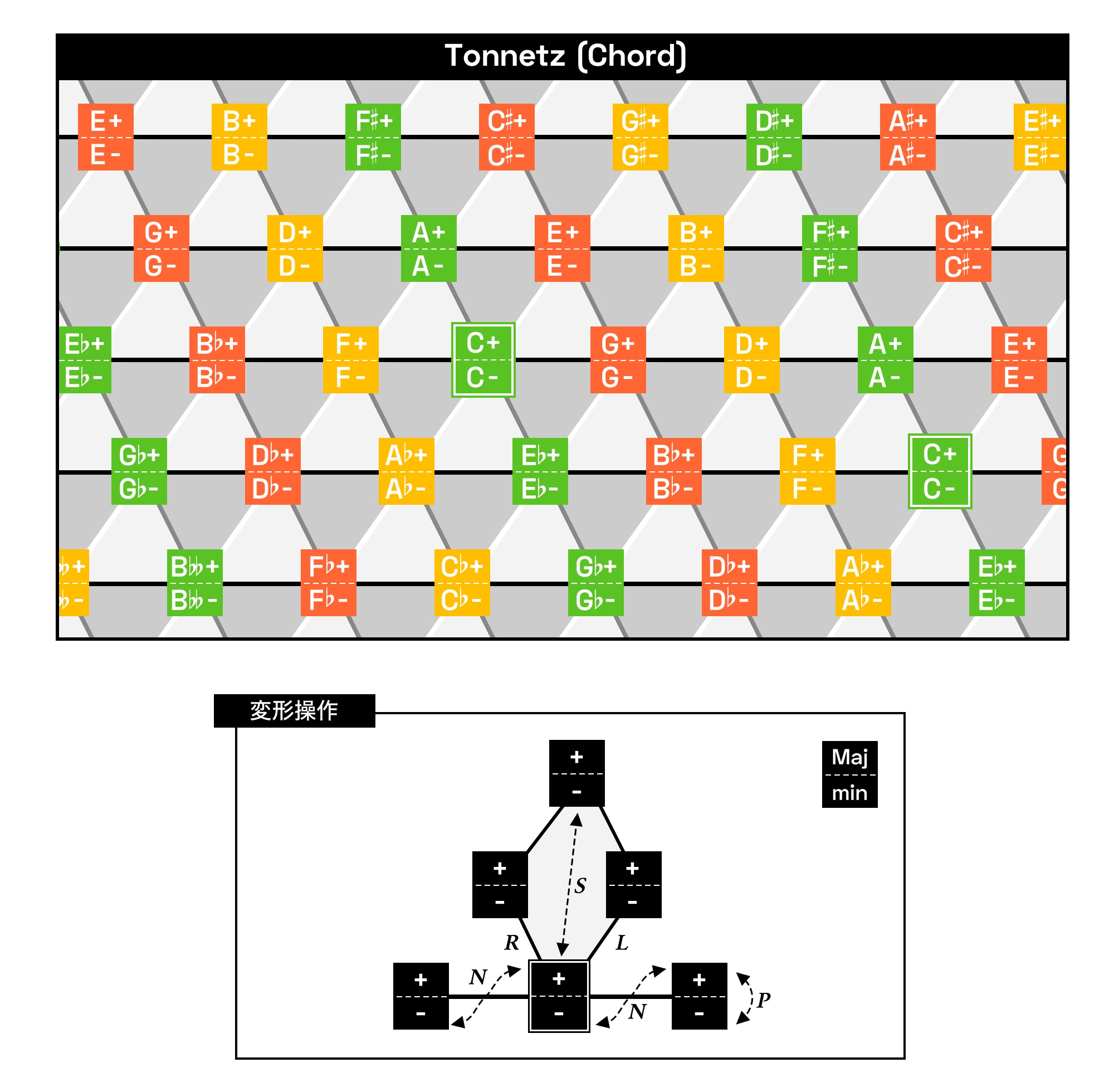
在新里曼理论中,大和弦通常表示为+,而小和弦则表示为-,这与数学类似,因此上图也遵循了这一点(在和弦理论中,+通常被称为aug,这让人困惑,但我们别无他法)。 在此图中,和弦的进行用直线上的移动来表示,这似乎比用平面来表示更简单。
4
超六音系统(Hyper Hexatonic System)
音网图声音铺在XY的平面上无限扩散,但在反映以一个八度循环的音乐世界时,有时还是画五度圈这样的圆环结构更直观。例如刚才勃拉姆斯的和弦进行也是A♭-G♯m-E-Em-C-Cm-A♭1个周期后返回原处。这是大3度的连续八度循环,如果有不是五度圈的“三度圈”,这种循环性就会变得简单易懂。
六音环
这也是个提案,首先制作如下的小圆圈。
这张图显示了L-P操作如何重复回到原点,总共列出了六个和弦,三个根音的大和弦和小和弦被大三度分开。可以说,勃拉姆斯的和弦进行是一个美丽的顺时针环形进行。
有趣的是,这些通过各有2个共同音的非常“节俭”的声部连接连接,所以制作这6个和弦所需的构成音也总共只有6个。
如你所见,这六个和弦可以用 c,e,g,b,e♭,a♭这六个音符来组成;六个音符可以组成六个和弦。这有点意思。这个圆环由6个音组成,所以叫做六音环(英 Hexatonic Cycle)8
*但是,关于把单音向内侧排列成圆形的魔法阵一样的图示方法,不是从先行研究中引用,而是本文独家的。
做四个环
自然地,可以用除 C、E和A♭之外的根音对创建相同的环。例如,如果通过提高半音将C♯、F 和A作为根音来创建一个环,则它将如下所示。
只是把刚才的图提高了半音,没有任何不可思议的地方。不过有趣的是,制作这6个和弦所使用的6个音中,c,e,g♯这3个音在刚才的环节中也出现过。
因为在上述的SLIDE操作中刚刚目击到作为C的3rd的e音也是C♯m的3rd,所以说也是理所当然的。这幅画有一种美,让人情不自禁地想去欣赏它……!
如果我们继续按照这个思路制作出包含D和E♭的音环,和弦的数量就是6 x 4 = 24,也就是说,12个根音每个包含大小的总共24个和弦。如果将所有内容放在一张图中,可以看到……
它看起来是这样的!通过将四个六音图排列起来,并将其中每个音程中使用的音高分组,形成一个维恩图,从而总结出24个和弦之间的关系,这个图被称为{term:(英 {term:超六音系统 (Hyper-Hexatonic System(HSS))9
*内侧没有单音信息,只是将六音环放置在东西南北的图叫做“六音系统”(同 p.17),这个图比那个高维,所以被命名为超六音系统。
在这张图中,首先L·P操作表现为圆环内的循环,根音的半音移动和5度行进是向旁边的环移动,全音移动和三音行进是向对面的环移动。另外,像C↔︎A♭m那样在环内朝对面移动的操作有特别的意义,所以取名为H(hexatonic pole)。这张图没有重视R操作的可视化。
六音环柱
考虑到R操作和5度关系的重要性,想要在某种程度上简单地图示这些连接时,将环状纵向重叠,将5度关系串起来,就会形成圆筒状的视觉效果,用简洁的线条将更多的操作连接起来。就能做到10

因为这是立体图形,所以在关系的表现力上更胜一筹。以5度连接为优先的情况下,上面的H0和下面的H0圆环的角度旋转120°,这也很有意思。
在这个图像上,例如刚才贝多芬的RL的连续进行就表现为圆筒侧面的一部分滑落的运动。
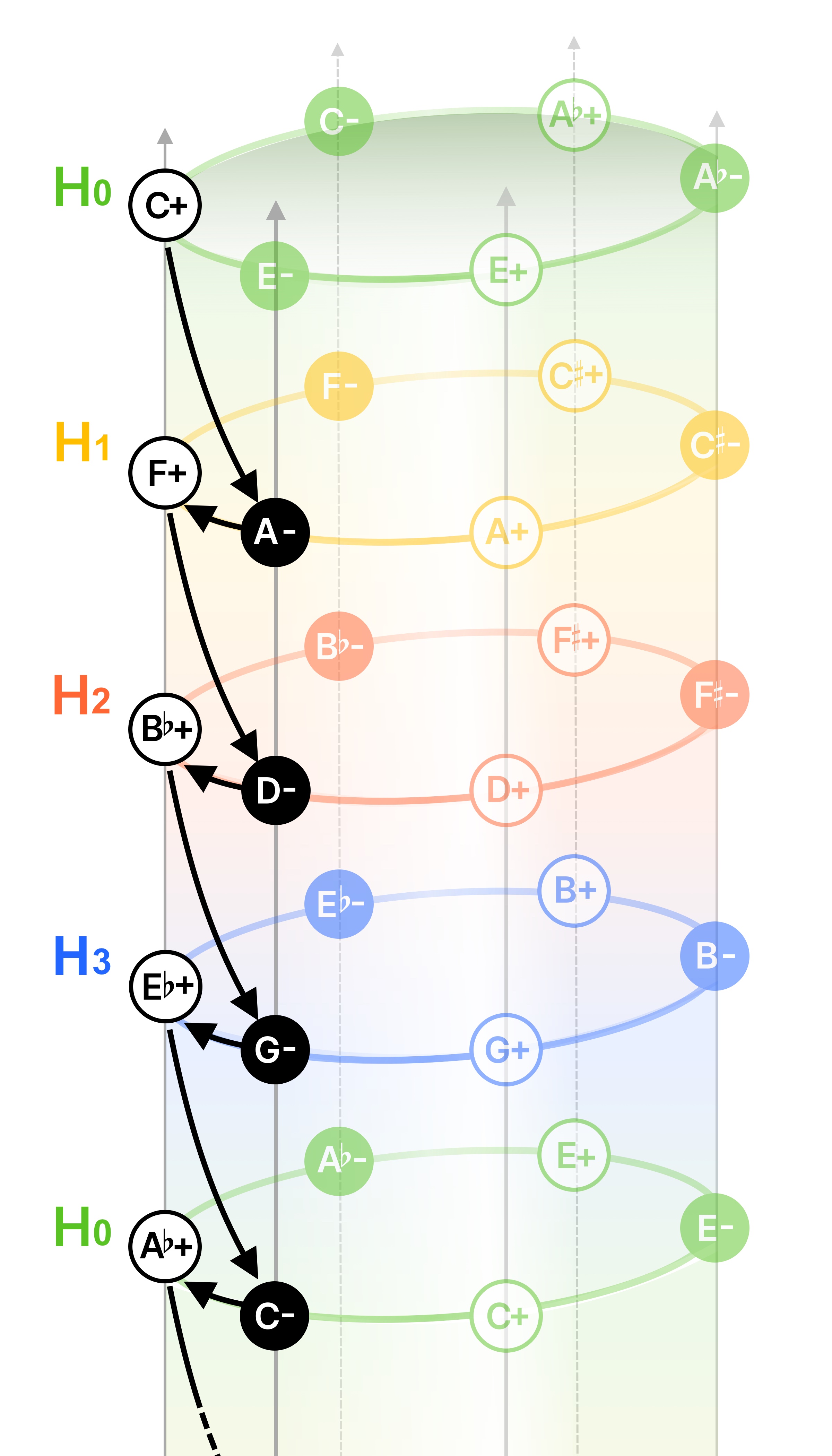
RL链的可视化
用这种方式进行分析固然有趣,但在制作过程中,将此图用作新和弦行进的提示也很有意思。
作为补充理论的意义
像这样,因为PLR的变形理论专门针对3度进行,它能够清晰地分离出优美的三度和半音衔接,否则在以五度为中心的理论中,这些进行和半音衔接会被视为微不足道。在以往的理论中,在分析中,关注V-I的动向也是最重要的,3度进行的地方往往被切断为单纯的同功能的延伸。聚焦于此的新里曼理论,作为补充传统理论的辅助工具时,似乎非常有用。
例如,关于转调,利用属系和弦和属七的推进力的转调是最具代表性的,而刚才在贝多芬的“第九交响曲”中看到的从Fm到D♭的平稳转调是基本的repertory不存在的。因此,如果只根据以往的理论进行分析的话,那个例子有可能会被当作“贝多芬果然是革新型的”那样的“例外”模式而被忽视。
然而,有了新里曼理论,这些例子就可以归类并收集在PLR的名称下,并可以作为基于例子的可复制技术付诸实践。
从这仅有的两个例子中,我们还可以感受到,在分析调性崩溃的19世纪浪漫主义时期的音乐时,它可能是有用的,因为它不需要指定调性(因此也不需要指定和弦的度数),因为重点只是和弦之间的联系。
在分析中确定调性,关注根音的变化,以五度进行为基础进行分析。这些都是传统理论的基本原则,但新里曼理论却与这些原则背道而驰。新里曼理论注重的是共同音的连接而非根音的变化,并以三度进行为基础。正因为新里曼理论与传统理论截然相反,它才吸引了如此多的兴趣和期望,成为发现迄今为止被忽视的问题的另一种工具。
“PLR操作”和“音网图”这两个新里曼理论中最具代表性的部分已经介绍完了,但像“六音环柱”这样的应用项目还剩下一些。但是,仅仅是到此为止的内容就应该有很多令人耳目一新的部分,所以我想在此稍作休息。
建设中。。。